密码学学习笔记

信息安全目标

三要素

机密性，完整性，可用性

攻击行为

截取(窃听),中断(拒绝服务),篡改,重放,伪造

五大安全属性

机密性

对应的攻击行为

截取/窃听

对应的密码技术

对称加密/公钥加密

完整性

对应的攻击行为

篡改

对应的密码技术

单向散列函数(hash)

可用性

对应的攻击行为

中断/拒绝服务攻击

对应的密码技术

/

不可否认性

对应的攻击行为

否认

对应的密码技术

数字签名

认证性

对应的攻击行为

伪造

对应的密码技术

消息认证码MAC

密码体制分类

密码学分为密码编码学与密码分析学

其中密码编码学根据安全目标分为:

认证体制

消息认证

认证消息真伪，保证消息源不被假冒

实体认证

验证身份，确保对方身份真实性

保密体制

对称密码体制

加解密使用同一套密钥

优点

扩张小(明文密文长度差不多)，易存储(密钥长度较短)，运算快

缺点

分发难(对信道安全要求高)，密钥数量大(n个人两两通信,要存储Cn2对密钥),难以解决不可否认性

公钥密码体制

优点

分发易(公钥pk是公开的),密钥数量小(每个人只需要公开自己的公钥pk，存储自己的私钥sk,n个人只需要管理n个密钥),有认证性(每个人的私钥只有自己知道)

缺点

运算慢(大多基于软件实现,对称密码可以依靠硬件实现),扩张大(往往需要在密文中添加其他中间参数以消除随机数影响),不易存储(密钥长度大)

柯克霍夫原则

秘密蕴藏于密钥之中，加解密算法安全性取决于密钥安全性，加解密算法过程和细节公开，只要密钥是安全的，攻击者就无法破译明文

安全体制评价

无条件安全

理论安全性

一次一密体制:密钥长度至少和明文长度一致的密码体制；1949年被香农证明无条件安全

缺点:密钥管理困难，现实不适应

优点：计算简单，难以破译

有条件安全

计算安全性

破译该密码算法在理论上可行，但现有算法与算力不可能完成攻击所需要的计算量

实际安全性

时间约束

破译所需时间不能超过该密码算法密钥的声明周期(不能花3min去破解一个生命周期只有1min的验证码)

成本约束

破译密码系统所需成本不能超过加密信息本身的价值(花1亿去破解只有10块余额的银行卡)

密码体制模型

密码体制/系统组成:{明文，密文，加密密钥，解密密钥，加密算法，解密算法}

• m:明文 M:明文空间
• c:密文 C:密文空间
• k1:加密密钥 K1:加密密钥空间
• k2:解密密钥 K2:解密密钥空间
• c = Ek1(m)
• m = Dk2(c)

密码体制安全性

破译密码体制

不知密钥，从密文推出明文/密钥

攻击方法

唯密文攻击

分析者手上只有一些截获的密文，根据这些密文推出明文/密钥

已知明文攻击

分析者手上不仅有相当数量的密文，同时还有一些明文密文对

选择明文攻击[加密机被暂时控制]

分析者手上不仅有相当数量的明文密文对，还能选择任意明文通过未知密钥获得对应密文

选择密文攻击[解密机被暂时控制]

分析者手上不仅有相当数量的明文密文对，还能选择任意密文通过未知密钥解密出对应明文

选择文本攻击[加密机和解密机都被暂时控制]

选择明文攻击和选择密文攻击的结合

攻击强度

唯密文攻击<已知明文攻击<选择明文攻击<选择密文攻击<选择文本攻击

能抵抗强度更高的攻击，自然可以抵抗强度低于它的攻击

现代密码要求

至少能抵御唯密文攻击和已知明文攻击

单表代换密码

明文中相同的字母在密文中都使用1个固定字母替换

基于密钥

给定一个字符串(eg:arrive)，将其中重复的字符去除，得到一个字母序列作为密钥(arive),明文密文映射规则如下:

a b c d e … z

a r i v e … z

将密钥字符串放到最前面，其他字母依次排序

仿射密码

明文x，密文y

加密:

​ y=ax+b (mod 26)

其中gcd(a,26) = 1 b是模26生成群中的一个元素

解密:

​ ax = y-b (mod 26)

​ x = a^-1(y-b) (mod 26)

当a=1，b=3时，就是凯撒密码

仿射密码的密钥空间：

b属于Z26,b有26种情况,gcd(a,26)=1,a有φ(26) = 1*12 = 12种

K = 26*12 = 312

多表代换密码

明文中的字母根据其出现的位置不同，在密文中被替换为不同字母

Hill密码

思想:明文密文转换构建在从字母到Z26群的映射

步骤

1.明文序列化

将明文字母映射到Z26上(A->0,B->1,…,Z->25),构建n行1列或1行n列的明文矩阵M (根据题目要求)

2.n*n密钥矩阵K

验证是否可逆 |K| != 0

3.加密

C=K*M mod26 (n行1列)

or

C=M*K mod26 (1行n列)

4.密文反序列化

C中的Z26群元素映射回字母

(0->A,1->B,…,25->Z)

Enigma密码机

构件

通过三个转子(26^3),接线板(10组线,10^16)提供了密钥空间

反射器使加解密算法相同

安全性

不能穷举攻击

密钥空间有26^3*10^16这么大

不能用字母频度分析

每次输入都会使转子转动，相同的字母会被加密成多种不同结果

传统密码分析

统计分析

一些字母/字母对出现的频率高于其他字母/字母对

明文密文对分析

对于Hill密码，若已知超过矩阵维数的明文密文对，就很容易破译

C=MK -> K=M^-1C

分组密码

将明文消息编码后得到的二进制序列划分成等长的块，在密钥控制下，每个块被加密成等长密文

设计原则

扩散

输入的明文每1比特的变化都尽可能多的影响输出明文的比特

混乱

加密过程中，明文、密文、密钥之间的关系尽可能变得复杂(像把他们扔到搅拌机搅碎了那样)

乘积密码

将简单的密码操作（轮函数）多次迭代，形成更强的混淆和扩散效果

迭代结构

Feistel网络结构

特点：输入会被分为等长的左右两部分

加密(Li表示左半部分,Ri表示右半部分,F()表示轮函数) i=0,1,2,…,n

​ Li = Ri-1

​ Ri = Li-1 xor F(Ri-1,Ki)

解密 i=n,n-1,…,1,0

​ Ri-1 = Li

​ Li-1 = Ri xor F(Li,Ki)

SP网络结构

S:代换 P:置换

通过多轮S代换和P置换交替迭代形成SP网络

S盒

起混乱作用；S盒是许多密码算法唯一的非线性部件，决定了密码算法的安全强度

P盒

起扩散作用(单置换不会起扩散作用，但是与多轮迭代和代换相结合，置换也起到了扩散作用)

雪崩效应

输入明文的微小变化也会导致输出密文产生显著变化

工作模式

ECB

特点:明文块独立加密(可并行加密)，相同明文块加密结果相同

只能用于加密小数据(只有一个分组或不足一个分组)，否则暴露统计特性，很危险

CBC

引入了初始向量IV，用于抗重放攻击

初始化向量IV xor 明文分组1的结果加密得到密文分组1

密文分组1 xor 明文分组2的结果加密得到密文分组2

…

CFB

与CBC不同的是，CFB是先加密在进行异或

初始化向量IV加密后，与明文分组1异或得到密文分组1

密文分组1加密后，与明文分组2异或得到密文分组2

…

OFB

对初始化向量IV做流加密(串行，但可预处理)

向量IV第i次加密的结果与明文分组i异或得到密文分组i

CTR

与OFB区别，OFB对初始化向量做流加密(串行),但是CTR使用计数器进行加密，是并行的

计数器并行生成加密的结果，与明文分组进行异或，得到密文分组

注意

1.ECB不能用来加密结构化数据(图片等)，因为ECB模式中，相同明文块的加密结果相同，这样一来会暴露明文模式

2.CBC模式的IV必须是随机且不可预测的，否则可能遭受选择明文攻击

3.CFB，OFB，CTR的IV或计数器不能重复使用

对称密码-DES

基本结构

分组密码算法，对称加密体制，加解密使用同一个密钥

分组长度:64位，不足64位的分组采取填充策略

密钥长度:64位，其中有效位数56位，第8k位(k=1,2,…,8)为奇偶校验位

迭代结果：Feistel网络结构(加解密结构相同，同一套软硬件实现)

加密

Feistel结构

初始64位明文分组m，经置换表IP后，分为等长32位的左右两部分,进行迭代，总共迭代16轮，最后一轮不再交换左右

先经过置换IP

1-15轮

Li = Ri-1

Ri = Li-1 xor F(Ri-1,Ki)

16轮

Ri = Ri-1

Li = Li-1 xor F(Ri-1,Ki)

密钥编排

初始密钥64位，经置换选择1后变为56位，循环左移输出56位，经置换选择2后变为48位，参与到加密的轮函数中

轮函数F

步骤可概括为E+SP

E

拓展，将长度为32位的半个明文块扩展到48位，便于与输入的48位密钥按位异或

+

将拓展后的半个明文块与密钥按位异或

S

进行S盒非线性字节代换（查表操作）；按位异或的结果为48位，分成8个组，对应8个S盒，每个分组长度为6位,表示为b1b2b3b4b5b6

查表规则如下:

行坐标:b1b6

列坐标:b2b3b4b5

将6位输入通过查表转换为4位输出

总体上就是，48位重新变为32位

P

P盒线性置换

安全性

由于单DES算法已不再安全，受限于兼容性等现实问题，发展出了多重DES用于解决DES的安全性问题

2DES

顾名思义，进行两次DES加密操作的DES

存在问题:中间相遇攻击

有效密钥长度为56位

从m->c1,计算复杂度为2^56,c2->c1计算复杂度为2^56

从这两个计算中找到 Dk1(m) == Ek2(c2),计算复杂度为2^56

总的复杂度约是2^57,相较与单DES，并没有显著提升安全性，因此2DES被淘汰

3DES

EEE3模式

使用3个不同密钥，加密三次Ek1()->Ek2()->Ek3()

密钥长度168位

EDE3模式

使用3个不同密钥,Ek1()->Dk2()->Ek3()

密钥长度168位

EEE2模式

使用2个不同密钥,Ek1()->Ek2()->Ek1()

密钥长度112位

EDE2模式

使用2个不同密钥,Ek1()->Dk2()->Ek1()

密钥长度112位

以EEE3为例，暴力破解的复杂度为2^168,如果采用中间相遇攻击，m->c1复杂度为2^56,c1->c2复杂度为2^56,那么m->c2复杂度为2^112,c3->c2复杂度为2^56,总的复杂度仍为2^168,不能被中间相遇攻击降低复杂度

优点:

1.密钥长度从单DES的56位增加到112位或168位，有效抗穷举攻击

2.升级成本低

缺点:

1.运算时间长，处理速度慢

2.密钥长度增加与明文长度不相匹配

对称密码-AES

基于SP网络结构(加解密结构不同，不能用同一套软硬件实现)，密钥长度128/192/256，对应迭代轮数10/12/14；分组长度128位

以AES-128为例

加密

每轮结构为:字节代换->行移位->列混合->轮密钥加

第1轮:轮密钥加->字节代换->行移位->列混合->轮密钥加

第10轮:字节代换->行移位->轮密钥加

字节代换

加密:S盒代换（16*16矩阵），1旧字节->1新字节，代换规则：

行坐标:1字节的高4位 列坐标:1字节的低4位

解密:逆S盒(16*16矩阵)

1旧字节->1新字节，代换规则：

行坐标:1字节的高4位 列坐标:1字节的低4位

行移位

128位明文块为16字节，转换为4*4矩阵

第一行循环左移0位，第二行循环左移1位，…,第四行循环左移3位

密钥拓展

128位密钥为16字节，转换为4*4矩阵

每列为一个字w[i]

拓展40个新列

w[i] = w[i-4] xor w[i-1] i=4k

w[i] = w[i-4] xor T(w[i-1]) i != 4k

T是一个复杂的函数

1.字循环:一个字中的4字节循环左移1位

2.S盒字节代换，规则与加密的相同

3.与轮常量Rcon[j]异或,j为轮数

解密

每轮结构：逆字节代换->逆行移位->逆列混合->轮密钥加

第1轮:轮密钥加->逆字节代换->逆行移位->逆列混合->轮密钥加

第10轮:逆字节代换->逆行移位->轮密钥加

逆字节代换

解密:逆S盒(16*16矩阵)

1旧字节->1新字节，代换规则：

行坐标:1字节的高4位 列坐标:1字节的低4位

逆行移位

128位明文块为16字节，转换为4*4矩阵

第一行循环右移0位，第二行循环右移1位，…,第四行循环右移3位

Hash函数

性质

单向性

对于给定的消息m，计算H(m)容易，（抗原像性）但是对于给定的H(m),推出原消息m在计算上不可行

抗碰撞性

碰撞:对于x!=y,有H(x)=H(y)

抗弱碰撞性

对于任意给定的消息x，找到y!=x且h(y)=h(x)在计算上不可行（更难找到）

抗强碰撞性

对于任意2个消息x!=y,找到h(x)=h(y)对应的(x,y)在计算上不可行

压缩性

对于任意长度的输入消息m，输出的消息摘要长度固定

应用

数字签名

通常h(m)的长度 << m的长度，对h(m)计算签名比对m计算签名更加高效

文件/程序指纹

对文件/程序生成哈希值，如果文件/程序被篡改，哈希值就会发生变化

安全存储/传输口令

涉及数据库存储的系统存储用户口令，通常不会存储明文，而是进行哈希压缩后存储，并且定期对其再进行哈希压缩

区块链交易的哈希值存到叶子节点

HMAC

基于Hash的消息认证码

密钥处理

与分组长度b相比：

• 密钥短:末尾补0
• 密钥长:通过当前HMAC实例选择的Hash算法压缩成长度为n的消息摘要

算法步骤

异或处理

密钥处理后得到k2

ipadkey = k2 xor ipad (ipad是0x00000036重复b/8次)

组合

m || ipadkey

哈希处理

h1 = hash(m || ipadkey)

异或处理

opadkey = k2 xor opad (opad是0x0000005C重复b/8次)

组合

h1 || opadkey

哈希处理

h2 = hash(h1 || opadkey)

输出MAC

输出h2

安全性

遭遇重放攻击：

​ 1.为消息赋予一个序号，双方同步更新

​ 2.时间戳:时钟一致（由于通信延迟存在并不能完全抵御）

​ 3.引入随机数，通信前先发送随机数（随机数生成计算开销；通信轮数增加）

暴力破解:

​ 1.限制单位时间内请求MAC验证的次数

​ 2.使用足够长的密钥

公钥密码-RSA

基于大整数分解困难问题

密钥生成

生成随机大素数p，q

计算n=pq

计算φ(n) = (p-1)(q-1)

引入随机数e作为公钥,gcd(e,φ(n))=1

计算私钥d，de = 1 modφ(n)

公钥(n,e),私钥d

加密

原消息m

c = m^e mod n

解密

m = c^d mod n

安全性

中间人攻击:对接收者伪装成发送者，对发送者伪装成接收者

效果:虽然没有直接破译RSA算法，但是破坏了消息的机密性且不易被察觉

中间人攻击成功的根本原因是:

1.缺乏身份认证，导致消息来源不详，攻击者可以伪装成任意身份

2.信道不安全，攻击者可以直接在信道中读写传输内容

公钥密码-ElGamal

基于离散对数困难问题

密钥生成

选择大素数p，在模p剩余类群Zp中找一个生成元g

选择一个随机数x作为私钥，计算公钥y = g^x mod p

加密

选取随机数a作为保密参数，计算A = g^a mod p

计算中间参数k = y^a mod p

对消息m进行加密，c = k*m mod p

密文为(A,c)

解密

m = c/A^x mod p

安全性

1.延展性攻击

截获密文A||C，对C扩大b倍

解密时 bC/A^x modp = bM

明文也被放大了b倍

2.主动/积极攻击

观察密文重复性，判断保密参数a是否重复

公钥密码-ECC

基于椭圆曲线上的离散对数困难问题

密钥生成

椭圆曲线群Ep(a,b)上选取一条椭圆曲线,找到生成元点G，阶为n(使nG = O的最小的n是一个素数)

选取随机数nb作为私钥(0<nb<n),计算公钥P=nbG

计算P不需要穷举，事实上，在椭圆曲线上计算kG，依据平衡二叉树进行计算，复杂度为logn

形如:

知道nb,2^m-1 <= nb <= 2^m，只需要计算m次

加密

选取随机数k

计算P1 = kG，P2=kP

选取随机点Pt=(xt,yt)

计算C = Mxt+yt

密文为 P1||P2+Pt||C

解密

Pt = P2+Pt-nbP1=(xt,yt)

M = C-yt / xt

安全性

ECC是公钥密码体制中安全强度最高的体制之一

ECC为什么没有完全替代RSA？

1.历史遗留问题，RSA已使用近50年，一些老旧系统只能支持RSA而不能原生支持ECC

2.ECC原理复杂，实现复杂度高

为什么公钥都是基于私钥生成的?

公钥密码体制的安全性依赖于公私钥计算的单向函数，从私钥推出公钥容易，但是从公钥推出私钥在计算上是不可行的；

公钥是公开的，如果私钥基于公钥生成，那么私钥就没有安全性可言了

基于私钥生成公钥，还能确保二者严格对应

公钥密码本质:利用数学上的单向函数，构造成一种由私钥推出公钥容易，而由公钥推出私钥在计算上不可行的密码体制

数字签名

实现方法:对消息的散列值进行签名(签名的消息不具有机密性)

对比直接对原消息签名，优势在于:

1.消息散列值的长度一般远小于消息本身长度，签名效率更高，开销更小

2.能抵御大部分伪造攻击；以RSA签名方案为例，如果直接对原消息签名，s1=m1^d mod p,s2 = m2^d mod p;攻击者构造新签名s3=s1*s2=(m1m2)^d mod p = m3^d mod p,在数学上是合理的

RSA数字签名

密钥生成

大素数p,q

计算n = p*q,φ(n)=(p-1)(q-1)

随机数e作为公钥，满足gcd(e,φ(n))=1

私钥d:de=1 modφ(n)

生成签名

选择安全hash函数h()

s = (h(m))^d mod p

与RSA加密不同(相反)的是，签名时使用私钥，验证时使用公钥

验证签名

验证s^e mod p是否与h(m)相等

Schnorr-ECC数字签名

密钥生成

选取椭圆曲线群Ep(a,b),选取椭圆曲线E，选取一个生成元点G，选取随机数nb作为私钥，生成公钥Pb = nbG = (xp,yp)

生成签名

选取随机数k，计算R=kG=(xr,pr)

生成签名s=k+h(Pb||R||m)*nb

验证签名

验证 sG与 R+h(Pb||R||m)*Pb

DSA

密钥生成

大素数p，q，满足p-1被q整除

选取随机数h，计算g=h^(p-1)/q modp

选取随机数x作为私钥，计算公钥y=g^x modp

生成签名

选择随机数k

计算r=g^k modp modq

计算s=(h(m)+xr)*k^-1 modp

验证签名

计算w=s^-1 mod p

计算u1 = h(m)*w mod p

计算u2 = r*w mod p

计算 v=g^u1 * y^u2 mod p 是否与r相等

特殊数字签名

盲签名

签名者对内容不可见

环签名

完全匿名

群签名

群成员可以代表群组签名，管理员可以溯源

门限签名

签名分为n个份额，超过t个参与者才能生成签名

不可否认签名

需要签名者配合认证，防止未授权认证

聚合签名

多个签名压缩为单个签名

密钥管理

生命周期

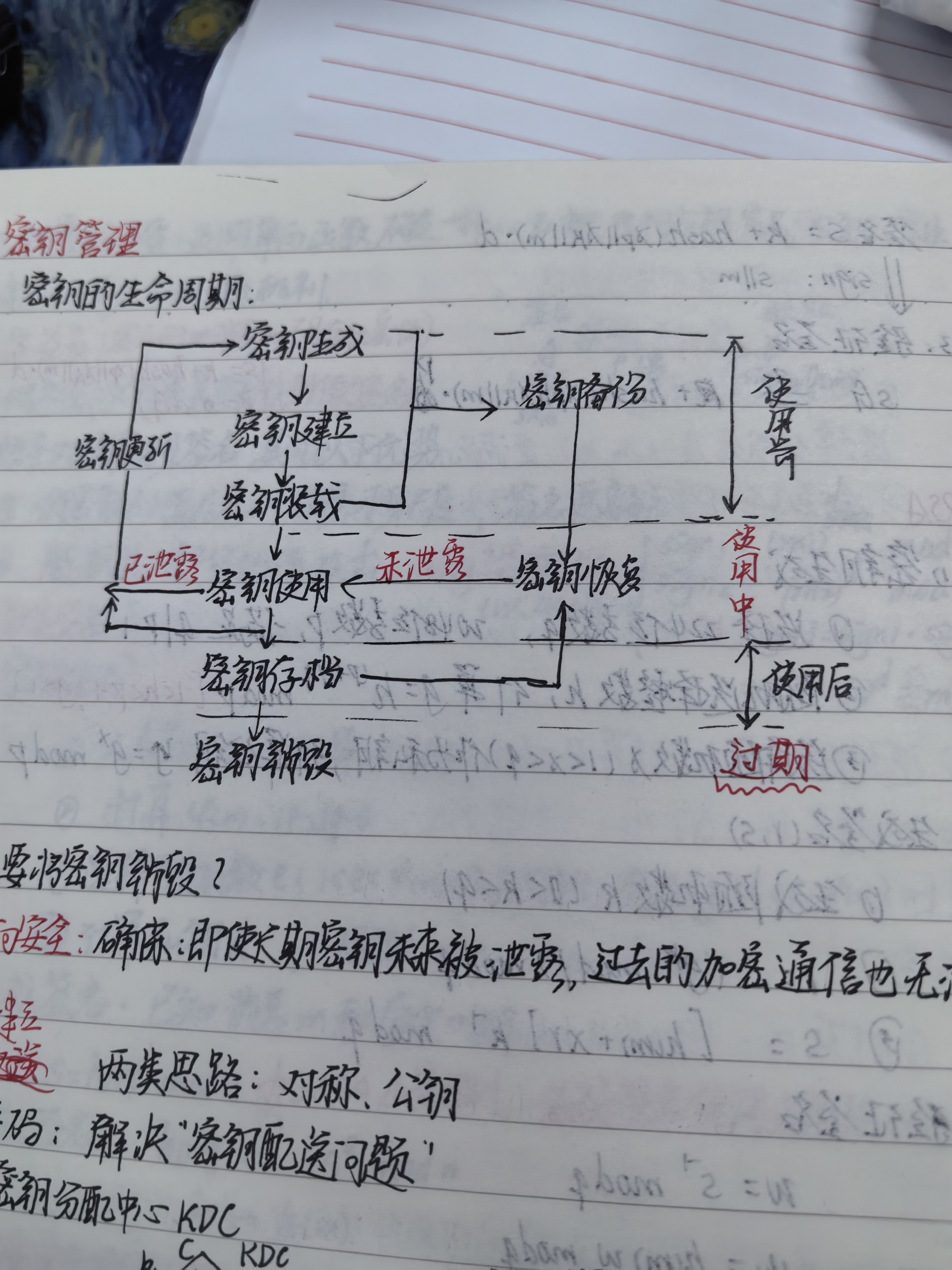
为什么要将密钥销毁?

为了前向安全

前向安全：确保长期使用的密钥即使泄露，过去加密的信息也不会被破译

密钥建立

对于对称密码

使用密钥分配中心KDC

核心思想

使用一个安全第三方(KDC)将双方通信所需的会话密钥分别用双方各自持有的密码加密后，再进行分发

步骤

1. A与B想进行安全通信(即使被窃听也不会泄露会话内容)
2. 于是，可信第三方C生成了二人的会话密钥kab；C将kab复制两份，一份用只有A知道的密码k1加密，另一份用只有B知道的密码k2加密
3. C将两份加密后的会话密钥统一发给A
4. A用自己的密码k1解密使用k1加密的kab，将自己想传输的信息m用kab加密后，连带着使用k2加密的kab一起发送给B
5. B收到使用k2加密的kab，使用自己的密码k2进行解密，得到kab；再对A使用kab加密后的消息m解密，得到原消息m

对于公钥密码

DH密钥交换协议 (密钥协商)

握手阶段

• 选择大素数p，模p剩余类群Zp上选择生成元g
• 公开p，g

协商阶段

• 对于Alice，选取随机数a作为保密参数，生成A=g^a mod p
• 对于Bob，选取随机数b作为保密参数，生成B=g^b mod p
• Alice将A发送给Bob，Bob计算会话密钥kba = A^b mod p
• Bob将B发送给Alice，Alice计算会话密钥kab = A^a mod p

最终得到会话密钥k=kab=kba=g^ab mod p

安全性

由于传输过程中缺乏对身份的认证，而且DH密钥交换协议是建立在双方在不安全信道上进行通信的情境下

会遭受中间人攻击

秘密共享技术

基本要求

• 将秘密S分成n个份额
• 已知t个份额容易还原出S
• 已知小于t-1个份额不能还原出S

当t<n时，称为(t,n)门限方案，泄露至多t-1个份额不会危及秘密S

Shamir (t,n)门限方案

步骤

• 参数选取:份额n，门限值t
• 秘密分割:选取t-1个随机数a1,a2,…,at-1;构造多项式s(x) = S+a1x+a2x^2+…+at-1x^(t-1) mod p
• 选n个整数x1,x2,…,xn，计算yi = s(xi)
• 将(xi,yi)通过安全信道分别发送给n个参与者
• 秘密恢复

$$
计算 ( S = P(0))：

S = \sum_{k=1}^{t} y_k \cdot \left( \prod_{\substack{1 \leq j \leq t \ j \neq k}} \frac{-x_j}{x_k - x_j} \right)
$$

密码协议

零知识证明协议

证明者向验证者证明某命题的真伪，证明过程中，除了证明该命题真伪，不告诉验证者其他任何信息

安全多方计算协议

满足以下条件

• 参与者将自己的秘密输入到某个多参数复合函数并计算该函数的值
• 满足某些安全属性，比如机密性
• 即使存在恶意输入，也要保证可靠性

不经意传输

发送者向接收者传输一些信息

其中：

• 发送者不知道接收者选择接收了哪些信息
• 接收者只能获取自己选择的信息内容，无法获取未选择的信息的内容

同态加密

对密文进行运算的结果进行解密，结果等同于对明文做相同的运算

eg：

​ c1=Ek1(m1),c2=Ek2(m2),c3=Ek3(m3)

​ D((c1+c2+c3)/3) = (m1+m2+m3)/3