Seq2Seq

定义

Seq2Seq是一个Encoder-Decoder结构的网络，它的输入是一个序列，输出也是一个序列，

Encoder使用循环神经网络(RNN,GRU，LSTM等)，将一个可变长度的信号序列(输入句子)变为固定维度的向量编码表达，

Decoder使用循环神经网络(RNN,GRU，LSTM等)，将这个固定长度的编码变成可变长度的目标信号序列(生成目标语言)

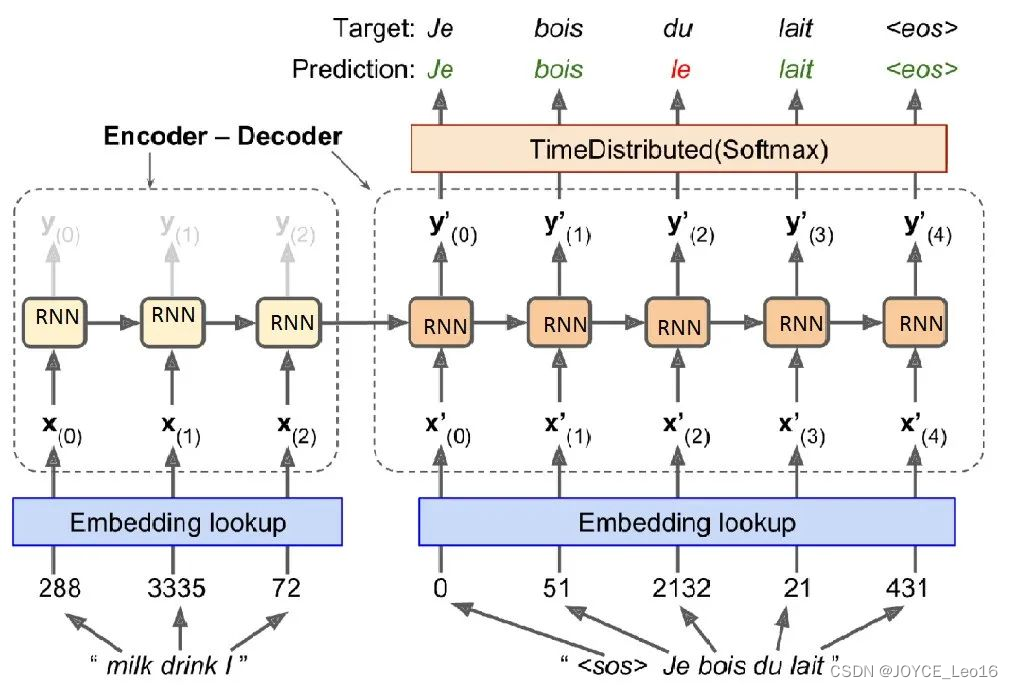
图中的圆角矩形即为cell：可以是RNN，GRU，LSTM等结构

相当于将RNN中的$h_0$输入Encoder (将Decoder部分理解成RNN，Encoder输出的Encoder state作为$h_0$)

Seq2Seq模型通过 端到端(？) 的训练方式，将输入序列和目标序列直接关联起来，避免了传统方法中繁琐的特征工程和手工设计的对齐步骤。这使得模型能够自动学习从输入到输出的映射关系，提高了序列转换任务的性能和效率

端到端(`End-to-End Learning`)

如何理解这个端到端(End-to-End Learning)？

输入序列到输出序列的全过程都由模型学习，我们不需要进行设计规则或特征

工作原理

Seq2Seq中的编码器使用循环神经网络将输入序列转换为固定维度的上下文向量，而解码器使用这个向量和另一个循环神经网络逐步生成输出序列

编解码器

编码器Encoder

把一个不定长的输入序列$x_1,\cdots,x_t$输出到一个编码状态$C$

编码过程中，编码器会逐个读取输入序列的元素，并更新其内部隐藏状态
编码完成后，编码器将最后一个输出的隐藏状态或经过某种变换的隐藏状态作为上下文向量/编码状态传递给解码器

解码器Decoder

输出$y^t$的条件概率将基于之前的输出序列$y^1,\cdots,y^{t-1}$和编码器输出的编码状态$C$

在每个时间步$t$上，解码器将根据上一个时间步的输出$y^{t-1}$,当前隐藏状态以及$编码状态C$来生成当前时间步输出$y^t$

作用

对于给定的输入序列$x_1,\cdots,x_t,\cdots,x_T$，使输出序列$y^1,\cdots,y^{t’},\cdots,y^{T’}$的条件概率值最大

就相当于求:
$$
\begin{align}
argmax(P(y^1,\cdots,\cdots,y^{T’}|x_1,\cdots,x_T))
\end{align}
$$

得到一组使条件概率最大的输出序列$y^1,\cdots,y^{t’},\cdots,y^{T’}$

最大似然估计

对于上面的做法，我们要使用最大似然估计来求出使得条件概率最大的输出序列$y^1,\cdots,y^{t’},\cdots,y^{T’}$

由于解码器的时间步输出值由前面的时间步输出以及当前时间步隐藏状态和编码状态C共同决定

最大似然估计为:

$$
P(y^1,\cdots,\cdots,y^{T’}|x_1,\cdots,x_T) = \prod_{t’=1}^{T’}P(y^{t’}|y^1,\cdots,y^{t’-1},C)
$$
多个概率连乘，最后的值会很小，不利于存储，进行取对数操作

$$
logP(y^1,\cdots,\cdots,y^{T’}|x_1,\cdots,x_T) = \sum_{t’=1}^{T’}logP(y^{t’}|y^1,\cdots,y^{t’-1},C)
$$

转换为使每个$y^{t’}$的条件概率最大的问题，最终得到最优的输出序列

注意力机制Attention Mechanism

核心逻辑

从关注全部到关注重点

Attention机制处理长文本时，能够抓住重点，不丢失重要信息
Attention机制类似于人类看图片的逻辑，会将注意力放在图片的焦点上

怎么做注意力

例子

比如对于这张图片，红色部分是人们更关注的

人看这张图片的过程可以描述为:人(查询对象Q(Query))看这张图片(被查询对象V(Values))，判断图片中哪些信息更重要，哪些信息更不重要(计算Q和V里事物的重要度(相关程度))

相似度计算

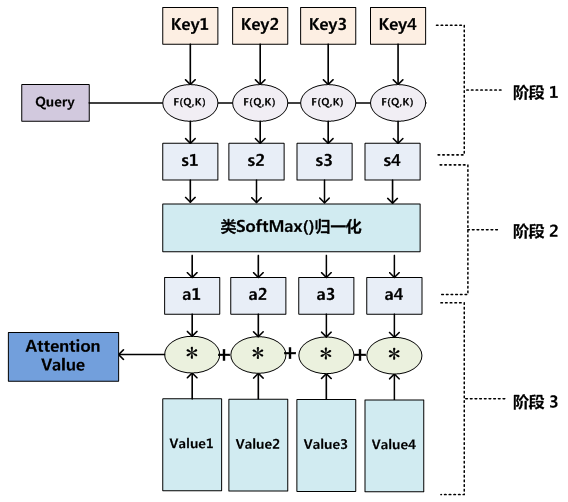
attention-计算图.png

K (Key)：与Q匹配的键，通过计算Q和K的相似度来得到注意力权重

类比:

Q:用户的搜索请求，比如搜索科幻电影
K:所有电影标签
V:电影本身内容

计算Q与K的相似度，得到权重向量，最终与V加权求和

方法

使用点乘的形式计算相似度$(i=1,2,…,n)$

$$
\begin{align}
f(Q,K_i) = Q^T\cdot K_i
\end{align}
$$

感知器

$$
\begin{align}
f(Q,K_i) = v^TTanh(W\cdot Q+U \cdot K_i)\
v，W，U:可学习的参数矩阵\
\end{align}
$$
权重点乘

$$
\begin{align}
f(Q,K_i) = Q\cdot W \cdot K_i \
W:可学习的参数矩阵
\end{align}
$$

权重拼接

$$
\begin{align}
f(Q,K_i) = W[Q;K_i] \
将Q和K向量拼接在一起，通过可学习参数矩阵W做线性变化
\end{align}
$$

softMax+归一化

$$
\begin{align}
\alpha_i = softMax(\frac{f(Q,K_i)}{\sqrt{d_k}})\
d_k:缩放因子，是Query向量和K向量的维度
\end{align}
$$
为什么要除以一个$\sqrt{d_k}$(？)

假设Q，K的每个元素是独立随机变量，均值为0，方差为1，那么点乘操作之后，均值为0，每个元素的方差为Q和K的维度$d_k$

当$d_k$很大时，分布就会集中在绝对值大的区域，造成概率两极化(接近0/1)，造成梯度消失

加权求和

$针对计算出的\alpha_i,对V中所有的value进行加权求和，得到Attention向量:$

$$
\begin{align}
Attention(Q,K,V) = \sum_{i=1}^{n} \alpha_i \cdot V_i = \sum_{i=1}^{n} softMax(\frac{f(Q,K_i)}{\sqrt{d_k}}) \cdot V_i
\end{align}
$$

seq2seq with Attention

在传统的seq2seq中有一个显著的缺点:

长句子问题

最初引入注意力机制是为了解决机器翻译中遇到的长句子(超过50字)性能下降问题

传统的机器翻译在长句子上的效果并不理想，本质原因是:

在Encoder-Decoder结构中，Encoder会将输入序列中的所有词统一编码成一个语义特征C后，再进行解码；因此C中就包含了输入序列的所有信息，它的长度就成了限制性能的瓶颈。对于长句子，语义特征C可能并不能存下所有的信息，造成了效果不佳

结构

在最初的seq2seq中，结构为

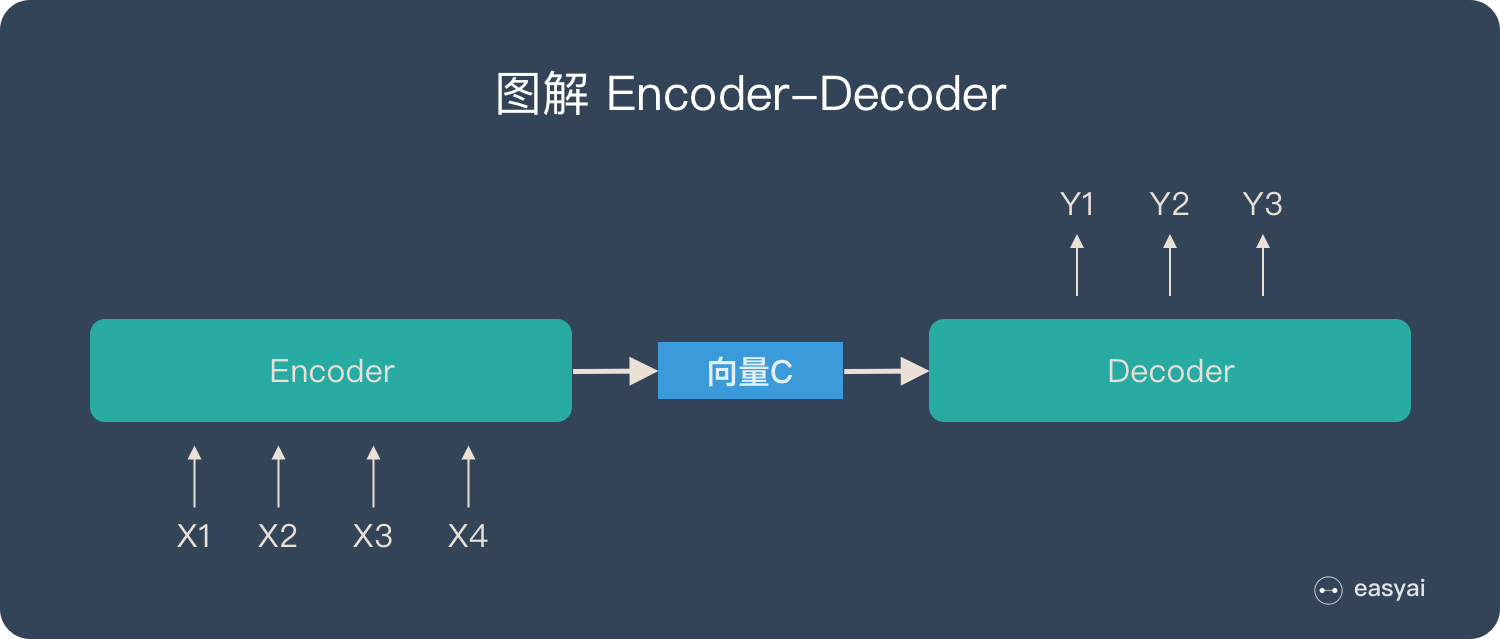
整个输入序列被编码为一个固定长度的编码状态C

而引入Attention机制之后，整个输入序列不再被编码成一个定长的编码状态C，而是编码成一个向量序列$C=[C_1,\cdots,C_n]$

核心在于:$C_i根据输出生成单词y_i不断变化$

从解码器输出的角度：

每个输出词y都会受到每个输入词x1，x2,x3,x4的影响，但是每个输入词对最终输出词y的影响权重不一样，这个权重由Attention计算得到

工作原理

此时Decodert时刻有3个输入: t-1时刻的隐藏状态输出和循环神经网络输出，以及Encoder输出的context-vec

编码器Encoder

结构

双向循环神经网络

在Seq2Seq with Attention的编码器中，使用了双向的RNN,GRU,LSTM结构，简称为RNNs

双向RNNs(BiRNNs)由前向RNNs和后向RNNs，分别处理序列前半部分和后半部分

比如对于”I love deep-learning”,通过BiRNNs可以同时知道love前面是I，后面是deep-learning

流程

输入处理
- 将语料分词后的token_id分批次传入embedding层，转换为词向量(Word2Vec形式，one-hot形式……)
特征提取
- 将前一步得到的词向量作为输入，传入Encoder的特征提取器-使用BiRNNs
状态输出
- 两个方向的RNNs都会产生隐藏状态输出，将这两个隐藏状态输出拼接，作为1个完整的隐藏状态输出h

解码器Decoder

结构

流程

隐藏状态
- 前一时刻的隐藏状态输出$s_{t-1}$
计算相似度score
- 计算前一时刻隐藏状态输出$s_{t-1}$与Encoder的第j步隐藏状态输出$h_j$的相似度score
计算注意力权重
- 将上一步的相似度score进行softMax归一化

计算上下文向量Context Vec

$$
得到的h_j与权重\alpha_{ij}进行加权求和，得到上下文向量
$$

公式

注意力分数计算

使用Decoder前一时刻隐藏状态$s_{t-1}$，Encoder中第j个时间步的隐藏状态$h_j$,进行计算得到注意力权重$\alpha_{ij}$

计算匹配得分

$$
匹配得分e_{ij}表示Decoder在第i-1步的隐藏状态输出s_{i-1}，与Encoder在第j步的隐藏状态输出h_j之间的匹配程度
$$

方法1:感知器
$$
\begin{align}
e_{ij} = v^T\cdot Tanh(W\cdot s_{i-1} + U\cdot h_j)
\end{align}
$$
方法2:使用二次型矩阵计算

二次型:一个向量和矩阵的乘积

$$
e_{ij} = s_{i-1}\cdot W_{i-1,j} \cdot h_j
$$

计算权重 $\alpha_{ij}$:

使用softMax函数进行归一化

$$
\alpha_{ij} = \frac{e_{ij}}{\sum_{i=1}^{n}e_{ik}}
$$

计算上下文向量 Context Vec

$$
\begin{align}
C_i = \sum_{j=1}^{n}\alpha_{ij}\cdot h_j \
n:序列长度\
C_i:解码步骤i的上下文向量\
\alpha_{ij}:输入序列中第j个词对解码步骤i的注意力权重\
h_j:编码器输出的第j个词的隐藏状态\
\end{align}
$$

比如对于”我爱机器学习” -> “I love machine learning”这个翻译过程

对于i=1，就是要计算 "I" 与 "我","爱","机器","学习" 每个时刻输入的相关性

类别

自注意力机制Self Attention

Self-Attention的关键点：Q，K，V都是来源于同一个序列X，通过X找到X里面的关键点

架构

Self-Attention 有3个输入 Q，K，V：

这三个输入来源于同一个输入序列X的词向量x的线性变换

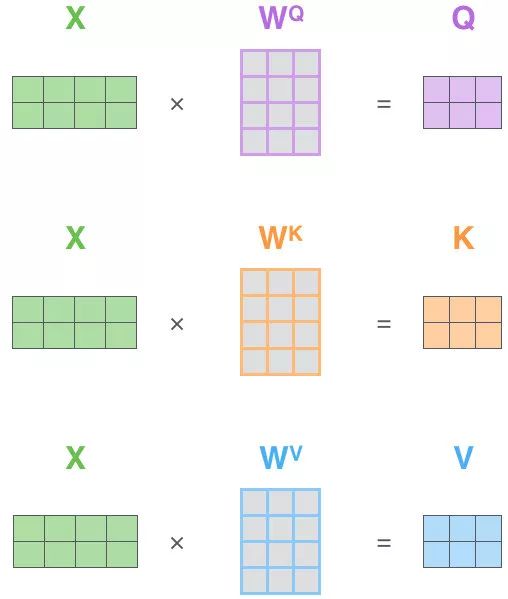
定义三个可学习的参数矩阵：$W_Q,W_K,W_V$

Q,K,V定义如下：
$$
\begin{align}
Q = x \cdot W_Q\
K = x\cdot W_K \
V = x\cdot W_V
\end{align}
$$

流程

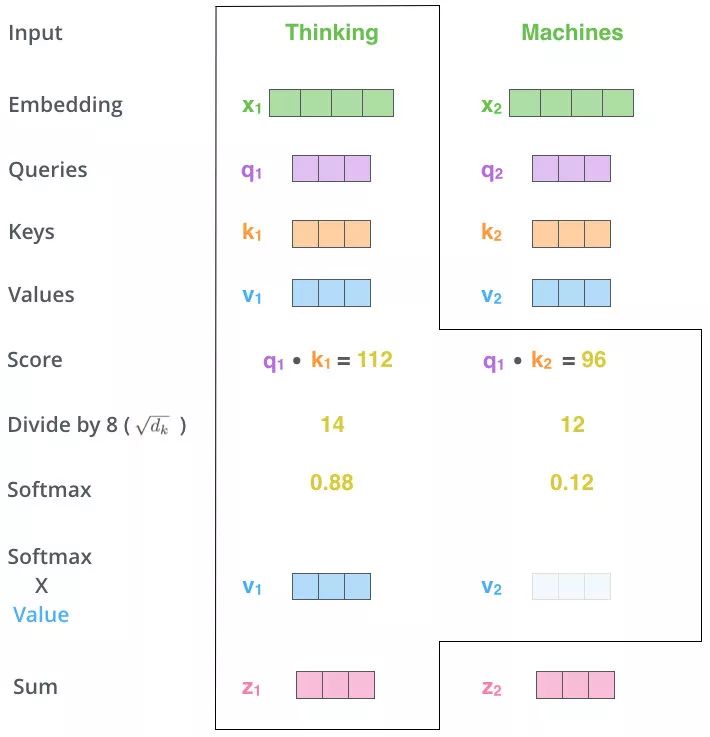
先以向量为例子：

得到初始的Q，K，V
$$
\begin{align}
对于序列X中第i个单词X_i的词向量x_i\ \ (i \ \in (0,n]):\
Q_i = x_i \cdot W_Q\
K_i = x_i \cdot W_K\
V_i = x_i \cdot W_V\
\end{align}
$$
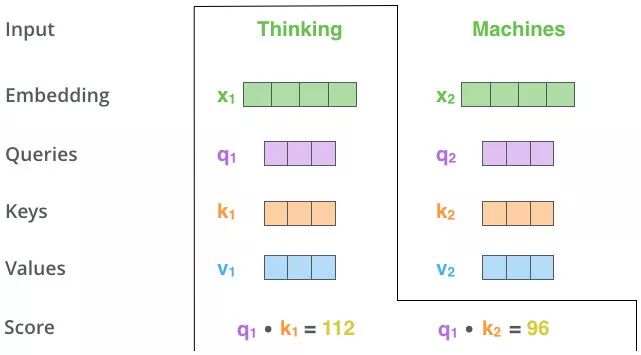
$计算当前查询Q_i与其他K_j(包括当前Q_i对应的K_i)的相似度$
$$
\begin{align}
使用点乘计算相似度:\
s_{ij} = Q_i \cdot K_j\ \ \ (i,j\ \in [0,n])
\end{align}
$$
归一化+softMax
$$
\begin{align}
需要对前面得到的s_{ij}进行归一化:除以缩放因子\sqrt{d_K}\
d_K:K的维度\
s_{ij}’ = \frac{s_{ij}}{\sqrt{d_{K}}}\
A_i = softMax(S’) = \frac{exp(s’{ij})}{\sum{k=1}^{n}exp(s’_{ik})}
\end{align}
$$

加权求和
$$
\begin{align}
Z_i = A_i \cdot V_i\
\end{align}
$$

以矩阵形式:

QKV-矩阵表示.jpg

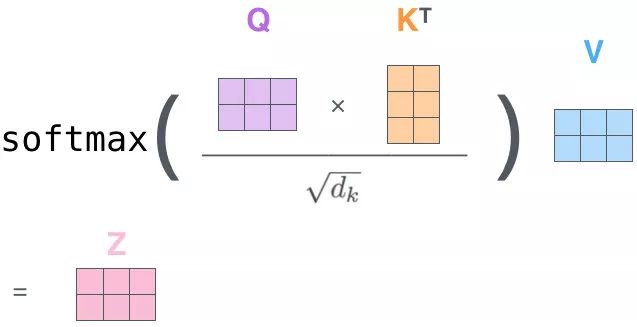
QKVZ-结果.jpg

对于这个softMax：

$$
\begin{align}
Q_i\cdot K_i^T是一个word2word的attention\ Map \
经过softMax后:\
矩阵内每个元素和为1，相当于每个元素之间都有对应的权重
\end{align}
$$
假设输入"I have a dream":

注意力机制矩阵图.jpg

形成了一张4×4的注意力图，每个单词与单词之间都有对应的权重

与普通Attention机制的区别

普通Attention:
- 在Encoder-Decoder模型中，查询向量Q是Decoder的输出，K和V位于Encoder
self Attention:
- 在Encoder-Decoder模型中，Q，K，V都是Encoder中的元素

与RNNs相比

self Attention 将任意两个单词通过一个计算步骤$Q_i\cdot K_j$动态联系在一起，不会存在RNNs中有效信息随时间序列推移而变得难以捕获的问题
并且RNNs计算是通过时间步序列进行串行，而self Attention可以对一句话中的每个单词单独的进行 Attention 值的计算，也就是说可以并行计算

Masked Self Attention掩码自注意力机制

架构

相较于self Attention:在归一化和softMax之间多了一层Masked操作

Masked指的是:在做语言模型(如机器翻译，文本生成…)时，不给模型看到未来的信息

假设在Masked之前，我们已经得到了一个attentionMap：

Masked要做的就是，只保留下三角矩阵

如这个形式：

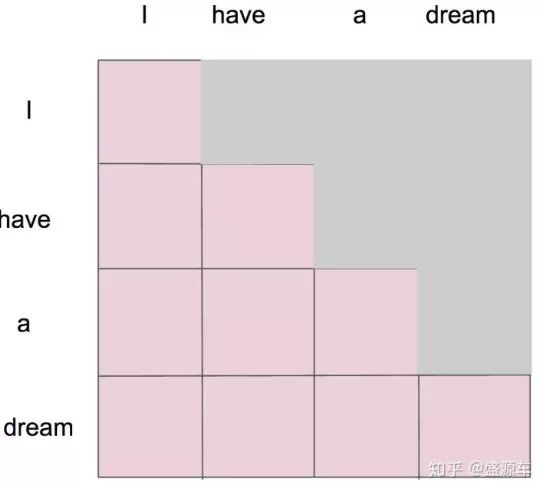
如何理解(？)

对于单一个单词”I”
- 只能和"I"自己有attention
对于第二个单词”have”
- 只能和"I"，"have"有attention
对于第三个单词”a”
- 只能和"I"，"have","a"有attention
对于第四个单词”dream”
- 只能和"I"，"have","a","dream"有attention

Masked后的attentionMap矩阵，经softMax处理后，横轴的attention weight之和为1

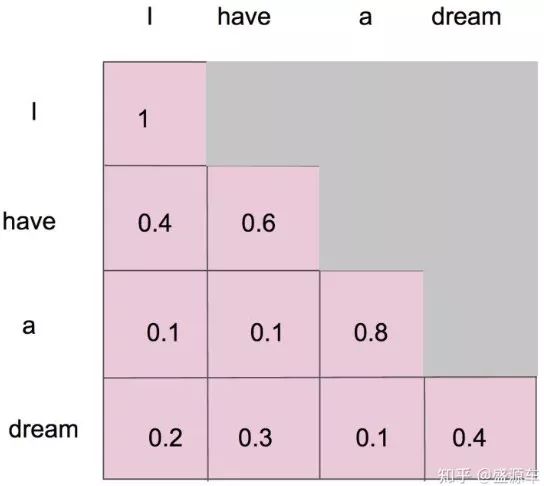
Attention(Q,K,V)计算公式变为：

$$
Attention(Q,K,V) = Z_i = softMax(\frac{s_{ij}}{\sqrt{d_K}}+Mask)\cdot V
$$

Multi-head Self Attention多头自注意力机制

回顾一下self Attention的整个流程：
$$
\begin{align}
对于序列X中第i个单词X_i的词向量x_i\ \ (i \ \in (0,n]):\
Q_i = x_i \cdot W_Q,
K_i = x_i \cdot W_K,
V_i = x_i \cdot W_V \
使用点乘计算相似度:\
s_{ij} = Q_i \cdot K_j\ \ \ (i,j\ \in [0,n]) \
s_{ij}’ = \frac{s_{ij}}{\sqrt{d_{K}}}\
A_i = softMax(S’) = \frac{exp(s’{ij})}{\sum{k=1}^{n}exp(s’_{ik})}\
Z_i = A_i \cdot V_i\
\end{align}
$$

所谓的多头，就是对于self Attention的加权求和得到的Z分割成n份 $Z_1,Z_2,\cdots,Z_n$

n通常取8

经过全连接层后，获得一个新的$Z’$

架构

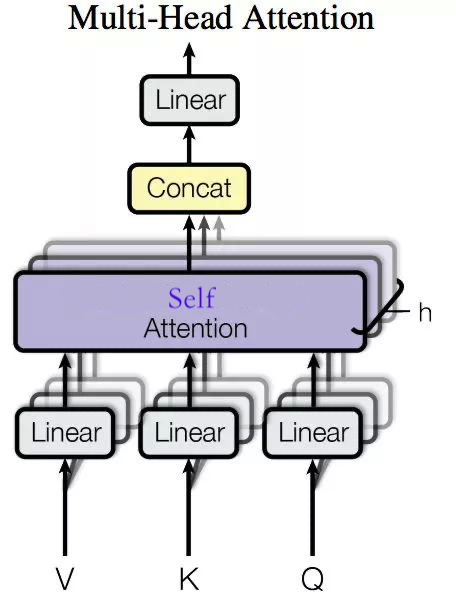
$输入序列x通过与h个不同的W_Q,W_K,W_V进行线性变换，得到h个不同的Q,K,V,最后得到h个Z,拼接后与另一个矩阵W进行线性变化后，得到Z’$

流程

定义多组W，生成多组Q，K，V
$$
\begin{align}
Q_{ik} = x_i\cdot W_{k}^{Q}\
K_{ik} = x_i\cdot W_{k}^{K}\
V_{ik} = x_i\cdot W_{k}^{V}\
k \in [0,h-1]
\end{align}
$$
得到多组Attention(Q,K,V)
$$
\begin{align}
s_{ik,jk} = Q_{ik}\cdot K_{jk} \
A_{ik} = softMax(\frac{s_{ik,jk}}{\sqrt{d_{K}}})\
Z_{ik} = A_{ik}\cdot V_{ik}\
\end{align}
$$
多组输出拼接后，与W0进行线性变换，降低维度
$$
\begin{align}
拼接:\
Z_i = concat([Z_{i1},Z_{i2},\cdots,Z_{ih}])) \
Z_i’ = W_0\cdot Z_i
\end{align}
$$

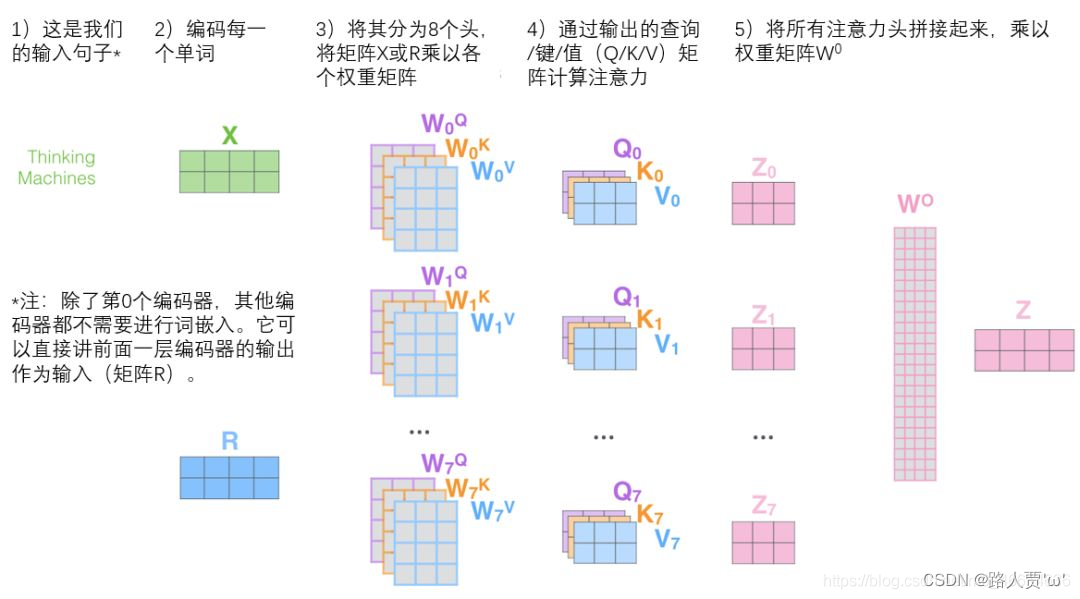
注意:除了第0个Encoder，其他Encoder都不需要进行word Embedding；它可以将前面一层Encoder的输出作为输入

为什么(？)学完Transformer的架构后解答

Seq2Seq

定义

端到端(End-to-End Learning)

工作原理

编解码器

编码器Encoder

解码器Decoder

作用

最大似然估计

注意力机制Attention Mechanism

核心逻辑

怎么做注意力

相似度计算

方法

softMax+归一化

加权求和

seq2seq with Attention

长句子问题

结构

工作原理

编码器Encoder

结构

双向循环神经网络

流程

解码器Decoder

结构

流程

计算上下文向量Context Vec

公式

注意力分数计算

计算上下文向量 Context Vec

类别

自注意力机制Self Attention

架构

流程

与普通Attention机制的区别

与RNNs相比

Masked Self Attention掩码自注意力机制

架构

Multi-head Self Attention多头自注意力机制

架构

流程

端到端(`End-to-End Learning`)